Blind Boxes
The “Blind Box” fashion in China
In recent years, the concept of “Blind Box” has become popular in China. Manufacturers sell boxes that contain one of $k$ different objects (often, figurines or cards) but do not give a hint which specific object is contained within. Customers wish to collect a complete set of all $k$ objects and therefore buy many of these “blind boxes.” Of course, while doing so they also obtain many duplicate objects.
The popularity of this fashion was described here. One very recent, attention-grabbing promotion was a collaboration of a fast-food chain and a toy manufacturer specializing in “blind boxes”. This was primarily criticised due to the potential for food wastage, when customers might buy food merely to obtain the toy figures within. Shortly after, the city of Shanghai announced regulations for “blind box" promotions.
Of course, this sort of marketing gimmick is not new and also quite amenable to treatment by probability theory.
The Coupon Collector Problem
The classic setting is that of a collector buying boxes of cereals, each box containing one of several existing “coupons.” It is assumed that the coupons are distributed randomly, with an equal probability for each box to to hold any given coupon. The primary question asks for the expected number of boxes that need to be bought to obtain one of each coupon.
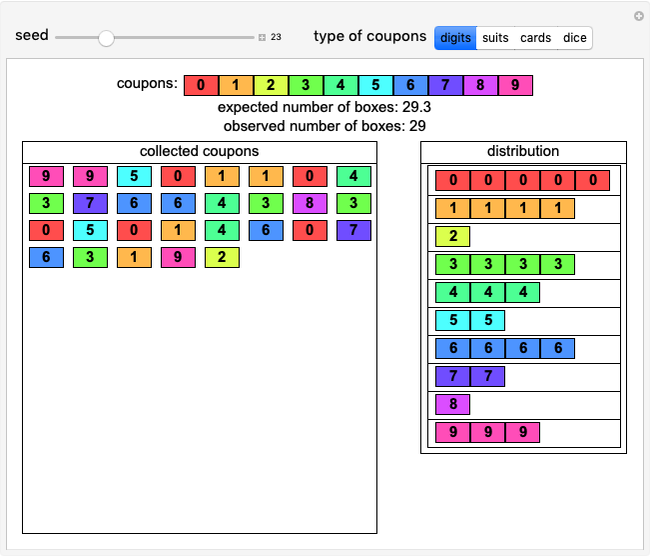
Yikai Teng "Simulating the Coupon Collector Problem”, Wolfram Demonstrations Project, Published: May 30, 2019
The above image shows a Mathematica simulation of coupon collection, downloadable at
https://demonstrations.wolfram.com/SimulatingTheCouponCollectorProblem/
Based on a total of 10 coupons, the randomly collected coupons are shown in the left-hand box while the right-hand box tallies them.
Some Exercises
Try to answer the following questions:
- Buying boxes until one obtains a given coupon can clearly be modeled by the geometric distribution. This approach for a single coupon can easily be adapted to that of collecting all of $k$ coupons. Show that if $X$ is the number of boxes needed to obtain all coupons, then $$\text{E}[X]=k\left(1+\frac{1}{2}+\dots+\frac{1}{k}\right).$$
- Using the inclusion-exclusion principle, give an expression for the probability that after buying $n\ge k$ boxes you have obtained all $k$ distinct coupons. This expression will be in the form of a summation that cannot be easily simplified.
- If $k=10$, calculate (using a computer) the probability that you will have to buy more than 30 boxes to obtain a complete set of coupons.
- It may seem that certain coupons are especially rare even if they are not. Suppose that you and a friend are both collecting $k=10$ coupons. How likely is it that after each of you buying $n_1=n_2=15$ boxes, that you are both missing one or more identical coupons? You may calculate the probability theoretically (this may be difficult) or use the above Wolfram simulation to conduct some experiments (note that the left-hand box of the simulation lists the obtained coupons in order, so you may simply look at the first 15 coupons to explore the question). You may summarize your simulation results and give a qualitative answer (e.g., "this happened often in our simulations”).
